Basic modeling example#

For the second example, we are going to model a fixed-rate mortgage loan, one of the basic types of amortized mortgage loans. In a fixed-rate mortgage, the borrower repays the same amount periodically for a certain term, such as 20 years or 30 years. To learn more about mortgage loans, Wikipedia has a great article detailing various types of mortgage loans.

For this exercise, we assume the payments are made annually. We model the annual payment amount using a well-known formula, for a given principal, interest rate and term. We also model the outstanding loan balance at each year throughout the payment term.

Through this second exercise, we are going to learn many new techniques, such as:

How to create a Model and Space explicitly,
How to set the Formula of an existing Cells,
What namespaces the Formulas of Cells are evaluated in,
What are References and how to define them,
How to interpret error messages,
How to change the values of References,
How to parameterize Spaces to create ItemSpaces.

For your reference, mortgage loans can also be modeled without using modelx. If you want to know how to model mortgage loans using Python and Pandas, check out great articles on the Practical Business Python site.

Creating a Model and a Space explicitly#

We start by creating a new MxConsole for this exercise. Right-click on the tab of the existing MxConsole or the default Console, and select New MxConsole.

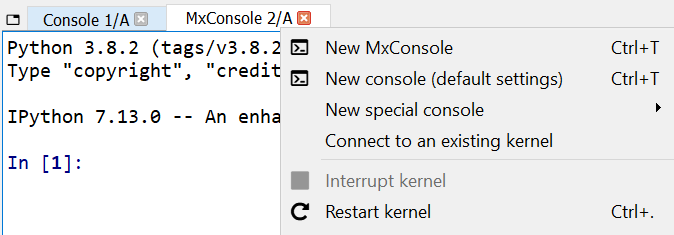
../_images/OpenNewMxConsole2.png — MxConsole Tab Context Menu#

A new MxConsole tab opens and after a few second, a new IPython session becomes ready to read your input in the MxConsole.

In the previous example, before creating a Cells, you did not explicitly create the parent Space or the Model for the Cells, but modelx automatically created them for you when the Cells was created. This time, we start by creating a Model and a Space explicitly, and name them Mortgage and Fixed.

Right-click in the blank MxExplorer, and select New Model. Enter Mortgage in the Model Name box in the dialog box. As you type Mortgage, the Import As box is also filled with Mortgage. This makes the Model accessible in the IPython in the MxConsole as a variable named Morgage. Click OK.

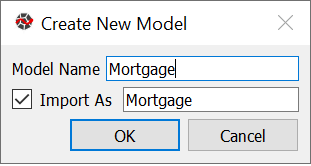
../_images/NewModelDialogMortgage.png — New Model Dialog Box#

Now you see Current Model - Mortgage is shown in the Model box at the top right corner of the MxExplorer.

../_images/ModelSelectorMortgage.png — Model Selector#

Next we are going to create a new Space named Fixed in Mortgage, which stands for fixed-rate mortgage.

Right-click in the blank MxExplorer, and select New Space. In the dialog box, you can see that Mortgage is selected in the Parent box. As there is no Space, only the Model can be the parent of the Space to be created.

Enter Fixed in the Space Name box. The Import As box should be filled with Fixed automatically.

The Base Spaces box is for inheriting other Spaces. We don’t cover the Inheritance concept in this exercise, so leave it blank here and click OK.

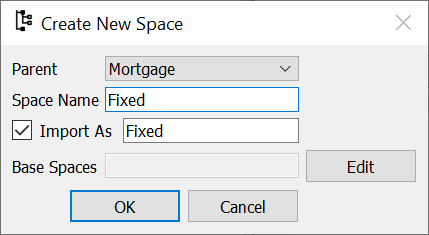
../_images/NewSpaceDialogFixed.png — New Space Dialog Box#

Now you should have the Fixed Space item in the MxExplorer.

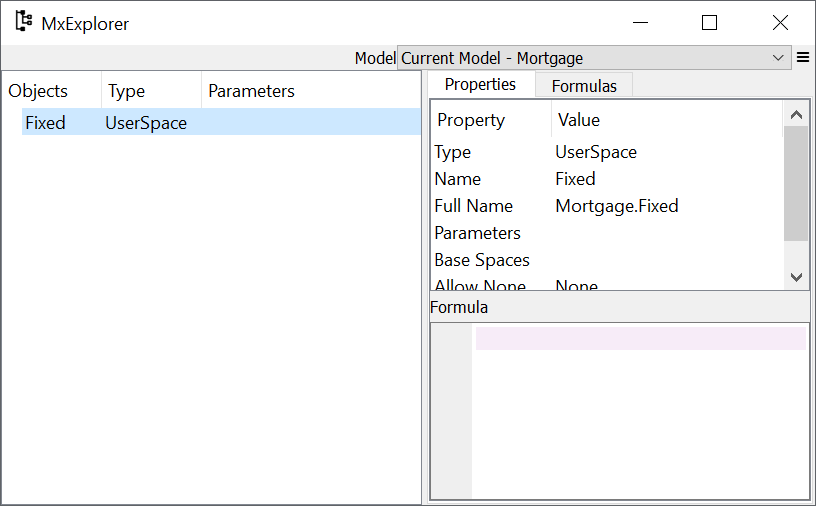
../_images/MxExplorerFixed.png — MxExplorer#

Creating Cells and defining their Formulas#

The annual payment for a fixed-rate mortgage can be calculated by a well-known formula and can be expressed as follows:

\[Payment = Principal\cdot\frac{Rate(1+Rate)^{Term}}{(1+Rate)^{Term}-1}\]

where $Principal$ is the principal amount borrowed, $Rate$ is the fixed annual interest rate on the outstanding loan balance and $Term$ is the length of the loan period in years.

This formula can be expressed in a Python function as follows:

def Payment():
    return Principal * Rate * (1+Rate)**Term / ((1+Rate)**Term - 1)

In Python ** in math expressions is the power operator, so the expressions (1+Rate)**Term above calculate (1+Rate) to the power Term.

Let’s create a Cells named Payment and define its formula by the function above. This time, let’s create it following steps different from the first exercise: We create Payment as an empty Cells, and assign the formula after it’s created.

Right-click on the MxExplorer, and select New Cells from the dialog box. Then enter Payment in the Cells Name box. As is always the case, leave the Import As check box checked to import Payment into IPython in the MxConsole. Click OK

../_images/NewCellsDialogPayment.png — New Cells Dialog Box#

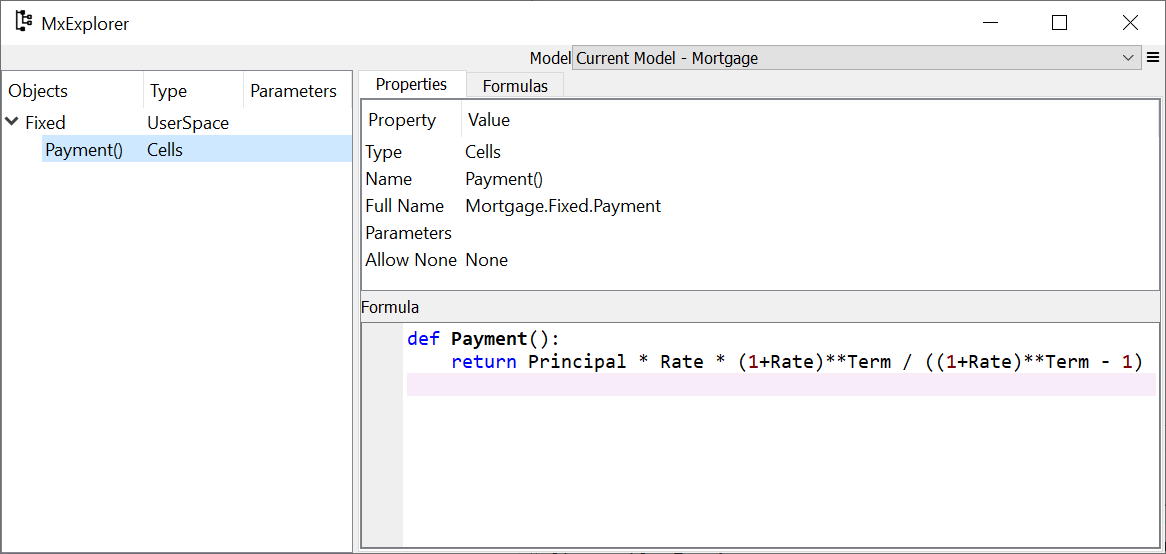
You can see the Payment Cells created under the Fixed Space in MxExplorer. Select the Payment Cells, right-click and select Show Properties item. The properties of the Payment Cells are shown in the Properties tab on the right side of the MxExplorer.

The expression lambda: None is set to the Formula property as the default formula. Enter the Payment function above in the Formula pane.

../_images/MxExplorerFixedPayment.png — MxExplorer#

The other item to calculate is the outstanding loan balance. Let $Balance(t)$ be the loan balance at time $t$. $Balance(t)$ can be expressed as the following recursive formula:

\[\begin{split}&Balance(t)=Balance(t-1)\cdot(1+Rate)-Payment\qquad&(0<t\leq{Term})\\ &Balance(0)=Principal\qquad&(t=0)\end{split}\]

The $Balance(Term)$ should be 0 if $Payment$ is calculated correctly by the previous formula.

As a Python function, the formula above can be expressed as follows:

def Balance(t):

    if t > 0:
        return Balance(t-1) * (1+Rate) - Payment
    else:
        return Principle

You may have noticed that the code above has a typo Principle, but let’s leave it as is to observe an error caused by the typo later.

Right-click on the MxExplorer, and select New Cells from the dialog box. Then enter Balance in the Cells Name box. Leave the Import As check box checked to import Balance into IPython in the MxConsole. Click OK

../_images/NewCellsDialogBalance.png — New Cells Dialog Box#

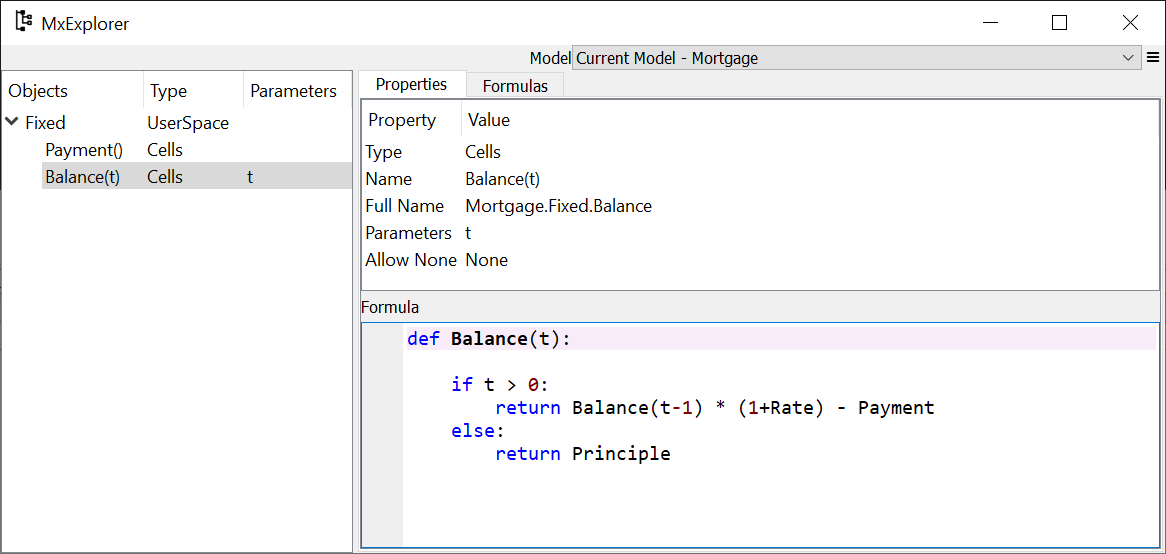
In the same way as you did for Payment, Open show the properties of Balance and put the function above in the Formula Pane.

../_images/MxExplorerFixedBalanceWrongFormula.png — MxExplorer#

Reading error messages#

The Payment Formula refers to names such as Principal, Rate and Term. We haven’t define those names yet, so calculating Payment should raise an error. Type Fixed.Payement() in the MxConsole and you should get the following error message:

FormulaError: Error raised during formula execution
NameError: name 'Principal' is not defined

Formula traceback:
0: Mortgage.FixedRate.Payment(), line 3

Formula source:
def Payment():

    return Principal * Rate * (1+Rate)**Term / ((1+Rate)**Term - 1)

The error message consists of 3 blocks of text. The first block shows the type and message of the original error. The original error in this case is NameError, as the name Principal is not defined.

The second block is Formula traceback. It shows the stack of Formula calls, as pairs of Cells and arguments, with the Formula you called on top, and the Formula call that raises the error at the bottom. In the case above, since the error is raised in the first Formula call, it only shows one Formula call, Payment().

The last block shows the Formula that raised the error.

Creating References#

The Payment Formula refers to the names Principal, Rate and Term so we need to define those names. Let’s assume the principal is $100,000, the interest rate is 3% and the payment term is 30 years.

You would think defining those names in the MxConsole as follows would work:

>>> Principal = 100000

>>> Rate = 0.03

>>> Term = 30

But actually it doesn’t. This is because, by the commands above you just define those names in the IPython’s global namespace. However, the Payment Formula is evaluated in the namespace associated with its parent Space, Fixed. In order for the Payment Formula to be able to refer to those names, you need to define References in the Fixed Space as below:

>>> Fixed.Principal = 100000

>>> Fixed.Rate = 0.03

>>> Fixed.Term = 30

You just created 3 Reference objects in the Fixed Space. A Reference object binds a name in its parent’s namespace to an arbitrary object.

Now you see that the 3 items are created in the MxExplorer. In the Type field, the types of Principal and Term are Ref/int, meaning that they are Reference objects, and the type of the associated values is int. In the same way, the type field of Rate shows Ref/float, which means that it is a Reference object, and the type of its value is float.

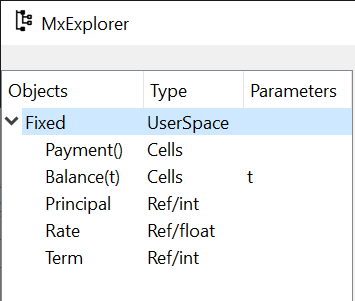
../_images/MxExplorerFixedReferences.png — MxExplorer#

Getting calculated results#

Now that you have defined all the References referenced by the Payment, calling the Formula should succeed:

>>> Payment()
5101.925932025255

To check the value is calculated correctly, we can make use of pmt function from numpy-financial package:

>>> import numpy_financial as npf

>>> npf.pmt(0.03, 30, 100000)
-5101.925932025255

You see that the absolute value of the returned value matches the Payment value.

Note

pmt function has been in numpy package, and it is still available in numpy, but it is deprecated and moved to a separate package numpy-financial. If you don’t have numpy-financial installed, pmt function may be available in numpy.

Next try getting the loan balance at year 30:

>>> Balance(30)

You should get the following error, as there is a typo in the formula.

FormulaError: Error raised during formula execution
NameError: name 'Principle' is not defined

Formula traceback:
0: Mortgage.FixedRate.Balance(t=30), line 4
...
28: Mortgage.FixedRate.Balance(t=2), line 4
29: Mortgage.FixedRate.Balance(t=1), line 4
30: Mortgage.FixedRate.Balance(t=0), line 6

Formula source:
def Balance(t):

    if t > 0:
        return Balance(t-1) * (1+Rate) - Payment()
    else:
        return Principle

The error message tells you that a NameError is raised in Mortgage.FixedRate.Balance(t=0) at line 6, because the name Principle is not found in the namespace in which Mortgage.FixedRate.Balance(t=0) is executed.

Correct the typo by going to MxExplorer and changing Principle to Principal in the Formula pane.

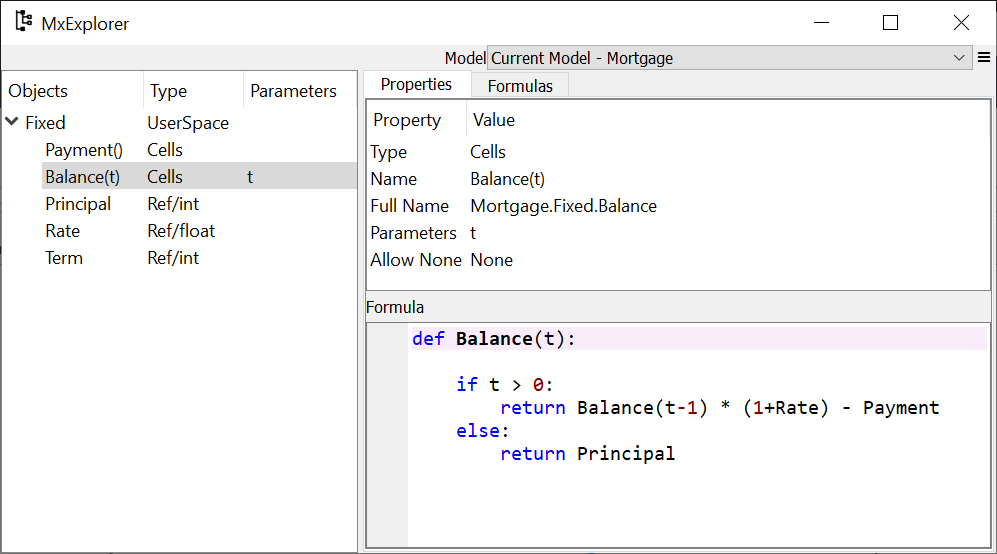
../_images/MxExplorerBalance.png — MxExplorer#

Calculate the balance again:

>> Balance(30)
1.2096279533579946e-10

The result is the reciprocal of 1.2 to the 10th power, which is effectively zero. It looks like the balance at each annual step till the year 30 is calculated correctly. You can check the values of the balance by dict(Balance) or Balance.frame, and also you can output a graph of the balance by:

>>> Balance.frame.plot()

You should get a line graph of the balance in Spyder’s Plots widget, and see that the line smoothly decreases till the year 30 where the balance becomes fully repaid.

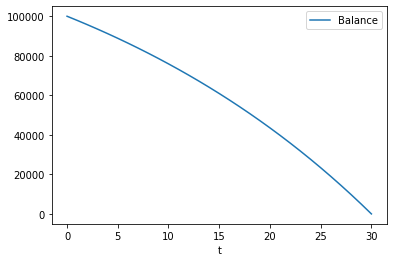
../_images/BalanceGraph.png — Mortgage Loan Balance#

Changing Reference values#

So far, we considered only one combination of principals, payment terms and interest rates. Usually, you want to explore other patterns as well. For example, you may want to know the annual payment amount when the payment term is 20 years.

To change Term from 30 to 20, assign 20 to Terms as follows:

>>> Fixed.Term = 20

The above changes the payment term to 20 years, and the values of Payment and Balance Cells are cleared because their calculations are dependent on Fixed.Term, except for Balance(0), which only depends on Principal. You can check how many values the Cells have by the len() built-in function:

>>> len(Payment)
0

>>> len(Balance)
1

To get the annual payment amount, simply call Payment:

>>> Payment()
6721.570759685908

The same applies to the interest rate. If you want to know what the payment is when the interest rate is 4%, assign 0.04 to Rate:

>>> Fixed.Rate = 0.04

>>> Payment()
7358.175032862885

When assigning a value to a Reference, be aware that you need to specify its parent Space, such as Fixed.Term = 20 and Fixed.Rate = 0.04 as explained in the previous section. Statements like Term = 20 and Rate = 0.04 will not work, because they are interpreted as just defining variables in the IPython’s global namespace.

Parameterizing the Space#

One drawback of changing Reference values to get results for various combinations of input is that, you can have results for only one combination of input at a time. If you update a Reference value, then the result for the previous value disappears. This is inconvenient if you want to use results from different combinations of input for subsequent calculations.

Space parameterization is a very powerful feature to quickly and naturally extend a Space written in terms of one combination of input into a parameterized Space. The parameterized Space supports the subscription operator([]) and the call operator(()). By passing arguments to the parameters through either of the operators, child Spaces of the ItemSpace type are dynamically created in the parameterized Space. The ItemSpaces are read-only Spaces and they inherit child Spaces, Cells and References from the parent Space, but the values of References that have the same names as the parameters are overridden by the arguments.

Using this feature, you can get results for any combinations of Term and Rate and maintain the results for all the combinations. To parameterize the Fixed Space by Term and Rate, assign a tuple of the Reference names to Fixed’s parameters property as follows:

>>> Fixed.parameters = ("Term", "Rate")

You can optionally give default values. For example, to give a default value of 30 to Term and 0.03 to Rate, execute the following assignment:

>>> Fixed.parameters = ("Term=30", "Rate=0.03")

Now the Fixed Space is parameterized by Term and Rate. By adding arguments to the Fixed Space as a subscription or call operators, a new child Space is created under the Fixed Space:

>>> Fixed[20, 0.03]
<ItemSpace Fixed[20, 0.03] in Mortgage>

The ItemSpace has the same Cells and References as the parent Space, except for the values of Term and Rate, which are set to the arguments:

>>> Fixed[20, 0.03].Term
20

>>> Fixed[20, 0.04].Rate
0.04

Let’s try to calculate Payment for various combinations of Term and Rate:

>>> Fixed[20, 0.03].Payment()
6721.570759685908

>>> Fixed[30, 0.03].Payment()
5101.925932025255

>>> Fixed[20, 0.04].Payment()
7358.175032862885

>>> Fixed[30, 0.04].Payment()
5783.009913366131

You can use () in place of [] in the code above. Since Term and Rate have default values, expressions like below yields the same ItemSpaces as above:

>>> Fixed[20].Payment()
6721.570759685908

>>> Fixed().Payment()   # Or Fixed[()].Payment()
5101.925932025255

>>> Fixed(Rate=0.04).Payment()
7358.175032862885

>>> Fixed[30].Payment()
5783.009913366131

In MxExplorer, you see that the ItemSpaces are created under the Fixed Space.

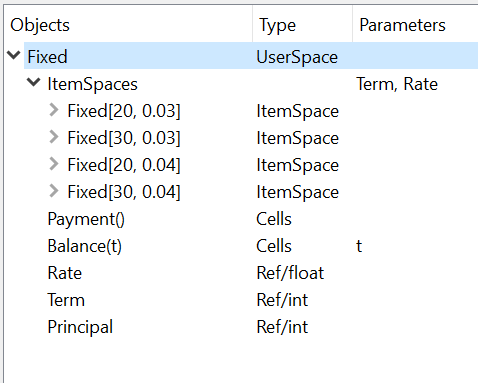
../_images/ItemSpaces.png — ItemSpaces in MxExplorer#

Open one of the ItemSpaces and you see that the Cells and References in the ItemSpace are the same as the parent Space, except for Term and Rate, whose values are set to the arguments of the ItemSpace.

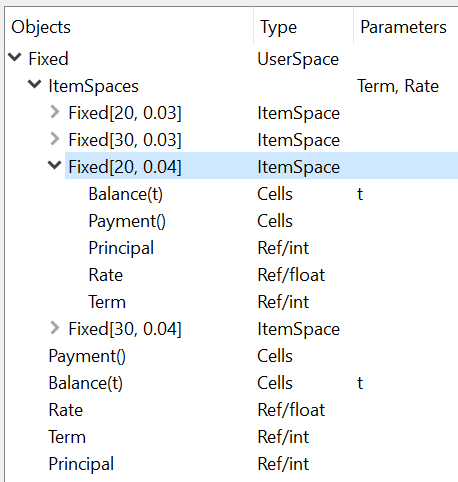
../_images/ItemSpaces2.png — ItemSpaces in MxExplorer#

Instead of manually specifying the arguments of the ItemSpaces, you can take full advantage of Python’s iterator and comprehension expressions. For example, suppose you want to compare the annual payment amounts for all the possible combinations of payment terms and interest rates, where the payment terms range from 20 years stepping up by 5 years to 35 years, and the interest rates from 2% to 4% by 1%. For this task, you can use the product iterator, available from the Python standard library. The code below shows how to get the desired results as a dict with tuples of Term and Rate as keys and Payment as values:

>>> from itertools import product

>>> {(term, rate): Fixed[term, rate/100].Payment() for term, rate in product(range(20, 36, 5), range(2, 5))}
{(20, 2): 6115.671812529034,
 (20, 3): 6721.570759685908,
 (20, 4): 7358.175032862885,
 (25, 2): 5122.043841739468,
 (25, 3): 5742.787103912777,
 (25, 4): 6401.196278645458,
 (30, 2): 4464.992229340292,
 (30, 3): 5101.925932025255,
 (30, 4): 5783.009913366131,
 (35, 2): 4000.2209190750104,
 (35, 3): 4653.929156959947,
 (35, 4): 5357.732236826054}

The code above use a form of expressions called dict comprehensions. If you’re not familiar with the expression, you can simply use for statement:

>>> result = {}

>>> for term, rate in product(range(20, 36, 5), range(2, 5)):
        result[(term, rate)] = Fixed[term, rate/100].Payment()

>>> result
{(20, 2): 6115.671812529034,
 (20, 3): 6721.570759685908,
 (20, 4): 7358.175032862885,
 (25, 2): 5122.043841739468,
 (25, 3): 5742.787103912777,
 (25, 4): 6401.196278645458,
 (30, 2): 4464.992229340292,
 (30, 3): 5101.925932025255,
 (30, 4): 5783.009913366131,
 (35, 2): 4000.2209190750104,
 (35, 3): 4653.929156959947,
 (35, 4): 5357.732236826054}

Saving the work#

You can save the Model in the same way we did in the fist exercise. From the context menu in MxExplorer, select Write Model and follow the same steps as the first example.

Note that the ItemSpaces in the Model are not saved, as they are dynamically created when you get them through the subscription or call operations for the first time. So, when you read the saved Model, the ItemSpaces do not exists, but they appear as you try to get them by the subscription or call operations, such as Fixed[20, 0.02].