Advanced usage#
Warning
This section is under review, and the contents may not be up-to-date.
This section covers more advanced modelx concepts and techniques that are not covered by the earlier sections.
Advanced Concepts#
In this section, more concepts we haven’t yet covered are introduced. Some of them are demonstrated by examples in the following section.
Space Members#
Spaces can contain cells and other spaces. In fact, spaces have 3 kinds of
their “members”. You can get those members as if they are attributes
of the containing spaces,
by attribute access(.) expression.
- Cells
As we have seen in the previous example, spaces contain cells, and the cells belong to spaces. One cells must belong to one ane only one space.
The
cellsproperty of Space returns a dictionary of all the cells associated with their names.- (Sub)spaces
As previously mentioned, spaces can be created in another space. Spaces in another space are called subspaces of the containing space. There 2 kinds of subspaces, static subspaces and dynamic subspace.
Static subspaces are those that are created manually, just like those created in models. There is no difference between spaces created directly under a model and static spaces created under a space, except for their parents being different types.
You can create a static subspace by calling
new_spacemethod of their parents:model, space = new_model(), new_space() space.new_space('Subspace1') @defcells def foo(): return 123
You can get a subspace as an attribute of the parent space, or by accessing the parent space’s
spacesproperty:>>> space.spaces['Subspace1'].foo() 123 >>> space.Subspace1.foo() 123
The other kind of subspaces, is dynamic subspaces. Unlike static suspaces, dynamic subspaces can only be created in spaces, but not directly in models.
Dynamic spaces are parametrized spaces that are created on-the-fly when requested through call(
()) or subscript([]) operation on their parent spaces. We’ll explore more on dynamic spaces in the next section, in conjunction with space inheritance by going through an example.- References
Often times you want access from cells formulas in a space to other objects than cells or subspaces in the same space. References are names bound to arbitrary objects that are accessible from within the same space:
model, space = new_model(), new_space() @defcells def bar(): return 2 * n
barcells above refers ton, which has not yet been defined. Withoutnbeing defined, callingbarwill raise an error. To define a referencen, you can simply assign a value tonattribute ofspace:>>> space.n = 3 >>> bar() 6
The
refsproperty of space returns a mapping of reference names to their objects:>>> list(space.refs.keys()) ['__builtins__', 'n', '_self']
Be default,
__builtins__and_selfare defined in any space. In fact,__builtins__is defined by default as a “global” reference in the model. Global references are names accessible from any space in a model. Other than the default reference, you can define your own, by simply assigning a value as an attribute of the model:>>> model.z = 4 >>> list(model.refs.keys()) ['z', '__builtins__'] >>> list(space.refs.keys()) ['z', '__builtins__', 'n', '_self']
__builtins__points to Python builtin module. It is defined to allow cells formulas to use builtin functions._selfpoints to the space itself. This allows cells formulas to get access to its parent space.
As mentioned earlier, formulas of cells are evaluated in the namespace that is associated with their parent spaces.
The namespace of a space is a mapping of names to the space members. As explained in the previous section, space members are either cells of the space, or subspaces of the space or references accessible from the space.
The table below breaks down all the members in the namespace by its types and sub-types.
cells |
self cells |
Cells defined in or overridden in the space |
derived cells |
Cells inherited from one of the base spaces |
|
spaces |
self spaces |
Subspace defined in or overridden in the space |
derived spaces |
Subspace inherited from one of the base spaces |
|
references (refs) |
self references |
References defined in or overridden in the space |
derived references |
References inherited from one of the base spaces |
|
global references |
Global references defined in the parent model |
|
local references |
Only |
|
parameters |
(Only in dynamic spaces) Space parameters |
Each type of the members has “self” members and “derived” members. Those distinctions stem from space inheritance explained in the next section.
Space Inheritance#
Inheritance in modelx is a feature analogous to class inheritance in object-oriented programming languages, such as Python. By making full use of space inheritance, you can organize multiple spaces sharing similar features into an inheritance tree of spaces, minimizing duplicated formula definitions, keeping your model organized and transparent while maintaining model integrity.
Inheritance lets one space use(inherit) other spaces, as base spaces. The inheriting space is called a derived space of the base spaces. The cells in the base spaces are copied automatically in the derived space. In the derived space, formulas of cells from base spaces can be overridden. You can also add cells to the derived space, that do not exist in any of the base spaces.
A space can have multiple base spaces. This is called multiple inheritance. The base spaces can have their base spaces, and derived-base relationships between spaces make up a directional graph of dependency. In case of multiple inheritance, we need a way to order base spaces to determine the priority of base spaces. modelx uses the same algorithm as Python for ordering bases, which is, C3 superclass linearization algorithm (a.k.a C3 Method Resolution Order or MRO). The links below are provided in case you want to know more about C3 MRO.
More complex example#
Let’s see how inheritance works by a simple code of
pricing life insurance policies.
First, we are goint to create a very simple life model as a space and name it
Life.
Then we’ll populate the space with cells that calculate the number of death
and remaining lives by age.
Then to price a term life policy, we will derive a TermLife space from
the Life space, and add some cells to calculate death benefits
paid to the insured, and their present value.
Next, we want to model an endowment policy. Since the endowment policy
pays out a maturity benefit in addition to the death benefits covered by the
term life policy, we derive a Endowment space from TermLife,
and make a residual change to the benefits formula.
Creating the Life space#
Below is a mathematical representation of the life model we’ll
build as a Life space.
where, \(l(x)\) denotes the number of lives at age x, \(d(x)\) denotes the number of death occurring between the age x and age x + 1, \(q\) denotes the annual mortality rate (for simplicity, we’ll assume a constant mortality rate of 0.003 for all ages for the moment.) One letter names like l, d, q would be too short for real world practices, but we use them here just for simplicity, as they often appear in classic actuarial textbooks. Yet another simplification is, we set the starting age of x at 50, just to get output shorter. As long as we use a constant mortality age, it shouldn’t affect the results whether the starting age is 0 or 50. Below the modelx code for this life model:
model, life = new_model(), new_space('Life')
def l(x):
if x == x0:
return 100000
else:
return l(x - 1) - d(x - 1)
def d(x):
return l(x) * q
def q():
return 0.003
l, d, q = defcells(l, d, q)
life.x0 = 50
The second to last line of the code above has the same effect as putting
@defcells decorator on top of each of the 3 function definitions.
This line creates 3 new cells
from the 3 functions in the Life space, and rebind names l, d,
q to the 3 cells in the current scope.
You must have noticed that l(x) formula is referring
to the name x0, which is not defined yet.
The last line is for defining x0 as the issue age
in the Life model and assigning a value to it.
To examine the space, we can check values of the cells in Life as below:
>>> l(60)
97040.17769489168
>>> life.frame
l d q
x
50.0 100000.000000 300.000000 NaN
51.0 99700.000000 299.100000 NaN
52.0 99400.900000 298.202700 NaN
53.0 99102.697300 297.308092 NaN
54.0 98805.389208 296.416168 NaN
55.0 98508.973040 295.526919 NaN
56.0 98213.446121 294.640338 NaN
57.0 97918.805783 293.756417 NaN
58.0 97625.049366 292.875148 NaN
59.0 97332.174218 291.996523 NaN
60.0 97040.177695 NaN NaN
NaN NaN NaN 0.003
Deriving the Term Life space#
Next, we’ll see how we can extend this space to represent a term life policy.
To simplify things, here we focus on one policy with the sum
assured of 1 (in whatever unit of currency).
With this assumption, if we define benefits(x) as the expected value at
issue of benefits paid between the age x and x + 1, then it should
equate to the probability of death between age x and x + 1, of the
insured at the point of issue. In a math expression, this should be written:
where \(l(x)\) and \(d(x)\) are the same definition from the preceding example, and \(x0\) denotes the issue age of the policy. And further we define the present value of benefits at age x as:
n denotes the policy term in years, and disc_rate denotes the
discounting rate for the present value calculation.
Continued from the previous code, we are going to derive the TermLife space
from the Life space, to add the benefits and present value calculations.
term_life = model.new_space(name='TermLife', bases=life)
@defcells
def benefits(x):
if x < x0 + n:
return d(x) / l(x0)
if x <= x0 + n:
return 0
@defcells
def pv_benefits(x):
if x < x0:
return 0
elif x <= x0 + n:
return benefits(x) + pv_benefits(x + 1) / (1 + disc_rate)
else:
return 0
The first line in the sample above creates TermLife space derived
from the Life space, by passing the Life space as bases parameter
to the new_space method of the model. The TermLife space at this point
has the same cells as its sole base space Life space.
The following 2 cells definitions (2 function definitions with defcells
decorators), are for adding the cells that did not exist in Life
space. The formulas are referring to the names
that are not defined yet. Those are n, disc_rate.
We need to define those in the TermLife space.
The reference x0 is inherited from the Life space.
term_life.n = 10
term_life.disc_rate = 0
You get the following results by examining the TermLife space (The
order of the columns in the DataFrame may be different on your screen).:
>>> term_life.pv_benefits(50)
0.02959822305108317
>>> term_life.frame
d q l pv_benefits benefits
x
50.0 300.000000 NaN 100000.000000 0.029598 0.003000
51.0 299.100000 NaN 99700.000000 0.026598 0.002991
52.0 298.202700 NaN 99400.900000 0.023607 0.002982
53.0 297.308092 NaN 99102.697300 0.020625 0.002973
54.0 296.416168 NaN 98805.389208 0.017652 0.002964
55.0 295.526919 NaN 98508.973040 0.014688 0.002955
56.0 294.640338 NaN 98213.446121 0.011733 0.002946
57.0 293.756417 NaN 97918.805783 0.008786 0.002938
58.0 292.875148 NaN 97625.049366 0.005849 0.002929
59.0 291.996523 NaN 97332.174218 0.002920 0.002920
60.0 NaN NaN NaN 0.000000 0.000000
61.0 NaN NaN NaN 0.000000 NaN
NaN NaN 0.003 NaN NaN NaN
You can see that the values of l, d, q cells are the same
as those in Life space, as Life and LifeTerm have exactly
the same formulas for those cells, but be aware that
those cells are not shared between the base and derived spaces.
Unlike class inheritance in OOP languages, space inheritance is in terms of
space instances(or objects), not classes,
so cells are copied from the base spaces to derived space
upon creating the derived space.
Deriving the Endowment space#
We’re going to create another space to test overriding inherited cells.
We will derive Endowment space from LifeTerm space. The diagram
below shows the relationships of the 3 spaces considered here.
A space from which an arrow originates is derived from the space the
arrow points to.

Life, TermLife and Endowment#
The endowment policy pays out the maturity benefit of 1
at the end of its policy term.
We have defined benefits cells as the expected value of benefits,
so in addition to the death benefits considered in LifeTerm space,
we’ll add the maturity benefit by overriding the benefits definition
in Endowment space. In reality, the insured will not get both death
and maturity benefits, but here we are considering an probabilistic model,
so the benefits would be the sum of expected value of death and maturity
benefits:
endowment = model.new_space(name='Endowment', bases=term_life)
@defcells
def benefits(x):
if x < x0 + n:
return d(x) / l(x0)
elif x == x0 + n:
return l(x) / l(x0)
else:
return 0
And the same operations on the Endowment space produces the following
results:
>>> endowment.pv_benefits(50)
1.0
>>> endowment.frame
pv_benefits benefits l q d
x
50.0 1.000000 0.003000 100000.000000 NaN 300.000000
51.0 0.997000 0.002991 99700.000000 NaN 299.100000
52.0 0.994009 0.002982 99400.900000 NaN 298.202700
53.0 0.991027 0.002973 99102.697300 NaN 297.308092
54.0 0.988054 0.002964 98805.389208 NaN 296.416168
55.0 0.985090 0.002955 98508.973040 NaN 295.526919
56.0 0.982134 0.002946 98213.446121 NaN 294.640338
57.0 0.979188 0.002938 97918.805783 NaN 293.756417
58.0 0.976250 0.002929 97625.049366 NaN 292.875148
59.0 0.973322 0.002920 97332.174218 NaN 291.996523
60.0 0.970402 0.970402 97040.177695 NaN NaN
61.0 0.000000 NaN NaN NaN NaN
NaN NaN NaN NaN 0.003 NaN
You can see pv_benefits for all ages and benefits for age 60
show values different from TermLife as we overrode benefits.
pv_benefits(50) being 1 is not surprising. The disc_rate
set to 1 in TermLife space is also inherited to the Endowment space.
The discounting rate of benefits being 1 means by taking the
present value of the benefits, we are simply taking the sum of
all expected values of future benefits, which must equates to 1,
because the insured gets 1 by 100% chance.
Dynamic spaces#
In many situations, you want to apply a set of calculations in a space, or a tree of spaces, to different data sets. You can achieve that by applying the space inheritance on dynamic spaces.
Dynamic spaces are parametrized spaces that are created on-the-fly when
requested through call(()) or subscript([]) operation on their parent
spaces.
To define dynamic spaces in a parent space,
you create the space with a parameter function whose signature is
used to define space parameters. The parameter function should return,
if any, a mapping of parameter names to their arguments,
to be pass on to the new_space method, when the dynamic spaces
are created.
To see how this works, let’s continue with the previous example.
In the last example, we manually set the issue age x0 of the policy
to 50, and the policy term n to 10.
We’ll extend this example and create policies as dynamic spaces with
with different policy attributes.
Assume we have 3 term life polices with the following attributes:
Policy ID |
Issue Age |
Policy Term |
|---|---|---|
1 |
50 |
10 |
2 |
60 |
15 |
3 |
70 |
5 |
We’ll create this sample data as a nested list:
data = [[1, 50, 10], [2, 60, 15], [3, 70, 5]]
The diagram shows the design of the model we are going to create.
The lines with a filled diamond shape on one end indicates that
Policy model is the parent space of the 3 dynamic spaces, Policy1,
Policy2, Policy3, each of which represents
each of the 3 policies above.
While Policy is the parent space of the 3 dynamic space,
it is also the base space of them.
Policy space inherits its members from Term model, and in turn
Policy is inherited by the 3 dynamic spaces.
This inheritance is represented by the unfilled arrowhead next the
filled diamond.
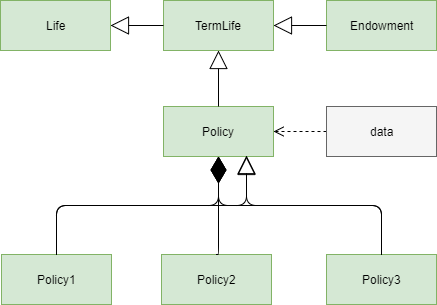
Below is a script to extend the model as we designed above.
def params(policy_id):
return {'name': 'Policy%s' % policy_id,
'bases': _self}
policy = model.new_space(name='Policy', bases=term_life, formula=params)
policy.data = data
@defcells
def x0():
return data[policy_id - 1][1]
@defcells
def n():
return data[policy_id - 1][2]
The params function is passed to the constructor of the Policy space
as the argument of formula parameter. The signature of params func
is used to determine the parameter of the dynamic spaces,
and the returned dictionary is passed to the new_space as arguments when
the dynamic spaces are created.
params is called when you create the dynamic subspaces of
Policy, by calling the n-the element of Policy.
params is evaluated in the Policy’s namespace. _self
is a spacial reference that points to Policy.
The parameter policy_id becomes available within the namespace of each
dynamic space.
In each of the dynamic spaces, the values of x0 and n are
taken from data for each policy:
>>> policy(1).pv_benefits(50)
0.02959822305108317
>>> policy(2).pv_benefits(60)
0.04406717516109439
>>> policy(3).pv_benefits(70)
0.014910269595243001
>>> policy(3).frame
n x0 d benefits l pv_benefits q
x
NaN 5.0 70.0 NaN NaN NaN NaN 0.003
70.0 NaN NaN 300.000000 0.003000 100000.000000 0.014910 NaN
71.0 NaN NaN 299.100000 0.002991 99700.000000 0.011910 NaN
72.0 NaN NaN 298.202700 0.002982 99400.900000 0.008919 NaN
73.0 NaN NaN 297.308092 0.002973 99102.697300 0.005937 NaN
74.0 NaN NaN 296.416168 0.002964 98805.389208 0.002964 NaN
75.0 NaN NaN NaN 0.000000 NaN 0.000000 NaN
76.0 NaN NaN NaN NaN NaN 0.000000 NaN
>>> policy.spaces
{'Policy1': <Space Policy[1] in Model1>,
'Policy2': <Space Policy[2] in Model1>,
'Policy3': <Space Policy[3] in Model1>}
Dynamic spaces of a base space are not passed on to the derived spaces.
When a space is derived from a base space that has dynamically created
subspaces, those dynamically created subspaces themselves are not passed
on to the derived spaces. Instead, the parameter function of the base
space is inherited, so subspaces of the derived space are created upon
call(using ()) or subscript (using []) operators
the derived space with arguments.
Reading Excel files#
You can read data stored in an Excel file into newly created cells.
Space has two methods new_cells_from_excel and new_space_from_excel.
new_space_from_excel is also available on Model.
You need to have Openpyxl package available in your Python environment
to use these methods.
new_cells_from_excel method reads values from a range in an Excel file,
creates cells and populates them with the values in the range.
new_space_from_excel methods reads values from a range in an Excel file,
creates a space, and in that space, creates
dynamic spaces using one or some of the index rows and/or columns
as space parameters, and creates cells in the dynamics spaces populating
them with the values in the range.
Refer to the modelx reference for concrete description of those methods.
Exporting to Pandas objects#
If you have Pandas installed in your Python environment, you can export values
of cells to Pandas’ DataFrame or Series objects.
Spaces have frame property, which generates a DataFrame
object whose columns are cells names, and whose indexes are
cells parameters. Multiple cells in a space may have different
sets of parameters. Generated
